Divide and Conquer
스미스차트(Smith chart) 본문
| 요약 | |
| 교류신호는 주파수의 역수에 비례하는 파장을 가지고 있다. 저주파의 경우 회로 설계 시 그 파장을 무시할 수 있다(근사) 고주파는 파형변화가 너무 빨라서 어떤 시점의 절대적인 전압, 전류값을 잡기 어렵다 =오실로스코프로 전압 파형을 관찰할 수 없음  |
|
| 상대적인 값으로 회로의 특성 파악 입력 전압파형이 들어갔을 때의 출력 전압 파형을 측정(전류*전압=전력 이용) 두 신호값을 서로 나눠 최대값의 비와 두 신호의 위상차를 구함 =네트워크 아날라이져(Network Analyser) 사용 |
|
| 이에 고주파 회로에서는 전력을 어떻게 효율적으로 전달이 중요하다. ➡(특성)임피던스 매칭(정합) 필요 |
|
| ※왜 효율적인 전달이 중요하지? 두개의 물탱크가 있고, 동일한 물의 양이 있으며, 호스의 굵기만 다르다고 가정해보자. (전하는 물의 양, 전압은 수압, 전류는 물의 흐름) 굵은 호스의 수압이 더 세서 좁은 호스의 물이 적게 흐른다 =신호를 보내주는 부분과 신호를 출력해 주는 안테나의 부분을 연결시 정재파 발생 정재파 진행파와 반사파가 동시에 존재하는 신호파 반사하는 신호가 많아지면 신호 약해짐 정재파비= 최대 전압/최소 전압 입력파와 반사파가 만났을때 그 지점에서 전압값이 변함 |
|
| ※임피던스 매칭이 뭔데? 두 호스의 굵기를 같게 해서 손실을 줄임 (특성임피던스 Z0=부하임피던스 ZL) = ZL/Zo=1 =출력 신호 최대 =전력의 효율을 최대화 =신호의 반사가 0 =반사계수 0 |
|
| ※어떻게 하는데? 스미트차트 이용 임피던스 매칭을 도와주는 하나의 도구 임피던스와 반사계수와의 관계를 도표화한 것 ➡Γ=중심에서 점까지의 거리/원의 반지름 거리 반사계수 크기 |Γ| < 1 반사계수 위상 -180˚< θ< 180˚ 주파수에 따른 임피던스 크기와 위상 측정 |
|
| 스미스차트=임피던스차트+어드미턴스차트 위 인덕터 영역, 아래 커패시터 영역 저항원R(실수)과 리액턴스원(허수)으로 이루어짐 복소좌표계 좌표상의 점=임피던스 →정규화 필요 (임피던스 차트 기준) L + 시계방향 0 ⊖ ∞ C |
|
| ※복소임피던스 수식 어드미턴스는 얼마나 신호를 더 잘 흘러줄 수 있느냐 임피던스=저항+리액턴스 어드미턴스=컨덕턴스+서셉턴스 |
|
| ※정규화가 왜 필요해? 스미스차트의 단위 안에 표현할 수 있도록 단위를 조절하는 과정 (log scale을 이용하여 0 ~ ∞까지의 복소좌표점을 하나의 원 안에 표현) ➡저항(0 ≤ r ≤ ∞) ➡리액턴스(-∞ ≤ x ≤ ∞) 어떤 특성임피던스에서도 동일하게 적용하기 위해 1이라는 임피던스 점을 기준으로 함 대부분 특성 임피던스 = 50Ω 중심점의 좌표는 1+j0=특성임피던스 =임피던스 매칭 매칭 후 실제물리적인 값을 알기 위해서는 초기 특성 임피던스를 다시 곱해 줘야 함 |
|
| ※용어 0 short 단락 도통 ∞ open 개방 L 유도성 직류O Lowpass 전압의 위상이 전류보다 뒤처지게 하는 소자 리액턴스 증가=서셉턴스 감소=인덕터 직렬 C 용량성 교류O Highpass 앞서게 하는 소자 |
|
| 산란계수(S-parameter) | 특정주파수에서 입력전압대 출력전압의 비 S11=전압 반사계수 S11이 낮을수록=반사가 적을수록 중앙에 모임 궤적이 위와 아래를 걸침=극점을 가짐 |



공부할 때 사용한 자료입니다
교류신호는 주파수의 역수에 비례하는 파장을 가지고 있다.
저주파의 경우 회로 설계 시 그 파장을 무시할 수 있다(근사)
그러나 고주파의 경우 신호의 위상과 진폭이 전혀 다르다.
또한 오실로스코프를 이용하여 간단히 전압 파형을 관찰할 수 없다.
따라서, 전류*전압=전력으로 회로의 특성을 측정한다.
이에 고주파 회로에서는 전력을 어떻게 효율적으로 전달이 중요하다.
따라서, 임피던스(특성 임피던스)를 정합시킬 필요가 있다.
스미스차트는 임피던스와 반사계수와의 관계를 도표화한 것으로, 임피던스 변환에 유용하다.
차트상에서는 임피던스(또는 어드미턴스)를 기준이 되는 특성 임피던스로 정규화하여 표시한다.
여기서 취급하는 주파수대에서는 대부분의 경우 특성 임피던스 50Ω을 기준으로 하고 있다.
http://www.ktechno.co.kr/rftech/rftech01.html
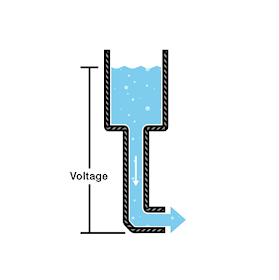
전압, 전류, 저항을 설명할때 보통 물탱크에 비유해서 설명한다.
(전하는 물의 양, 전압은 수압, 전류는 물의 흐름)
탱크속의 물은 전하를 의미한다.
호스 끝의 압력이 전압을 의미한다.
탱크속에 물이 더 있다면, 더 높은 전하를 가진것이고 더 높은 압력이 측정될 것이다.
(호스를 열면 수압에 의해 물이 흘러 나가고, 수압이 점차 줄어든다 = 물탱크를 배터리라고 생각했을 때 배터리 전압이 떨어져서 전등 빛이 어두워지는 것)
=호스로 빠져나간만큼 물이 줄어드는데 낮은 압력은 적은 물이 흐르고 있다는 뜻이다.
호스를 통해 흘러나온 물의 양을 전류라고 생각할 수 있다.
압력이 높으면 많이 흐른다.
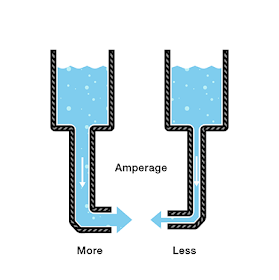
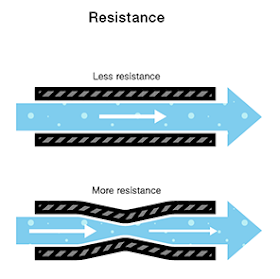
이제 두개의 물탱크가 있고, 동일한 물의 양이 있으며, 호스의 굵기만 다르다고 가정해보자.
각각 동일한 양의 물이 들어있지만 탱크를 열어두면 좁은 호스쪽이 물이 적게 흐른다. (=좁은 호스가 전류가 작다)
전류를 키우려면 물을 늘려야 한다=압력을 늘린다=물이 더 많이 빠져나간다=전압 증가로 전류 증가
좁은 호스쪽은 넓은 호스쪽과 같은 압력이지만 물의 흐름에 방해가 있다.
https://jbelec.blogspot.com/2020/01/blog-post.html?m=1
1. 전압 반사계수는 S11 과 같다.
2. 임피던스 Matching(ZL=Zo)이 되면 반사계수는 0이다.
즉, 이때가 Signal Integrity 측면에서 가장 좋다.
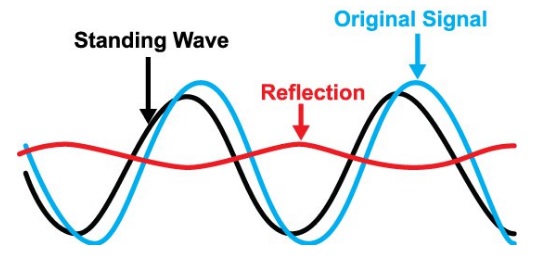
3. 전압 정재파비란 최대 전압/최소 전압이다.
이것의 의미는 입력파와 반사파가 만났을때 그 지점에서 전압값이 변하기 때문이다.
파란신호를 넣어줬는데 빨간색 반사되는 신호때문에 실제로는 검은색 신호가 전달된다는 개념이라고 보면 된다
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=narabaljeon&logNo=220791531068
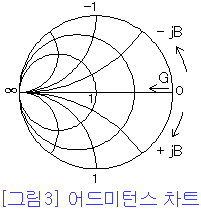
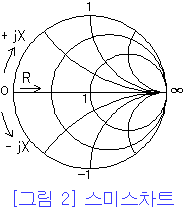
http://www.ktechno.co.kr/rftech/rftech01.html
- 복소좌표계를 log scale로 나타낸 것
- 0 에서 무한 대까지의 복소좌표점을 하나의 원 안에 완벽하게 표현 가능
- 반사계수와 임피던스가 서로 변환된다는 관계를 이용
- 임피던스을 알면 반사계수를 즉시 알 수 있고, 역으로 반사계수를 알면 바로 특성임피던스를 알 수 있는 일종의 툴
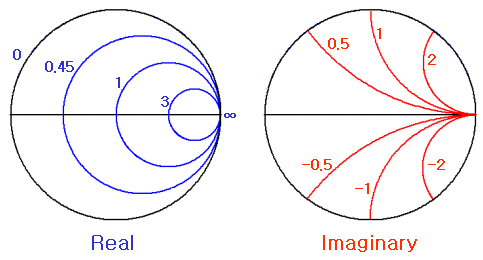
- 스미스챠트는 저항원과 리액터스 원으로 구성됨
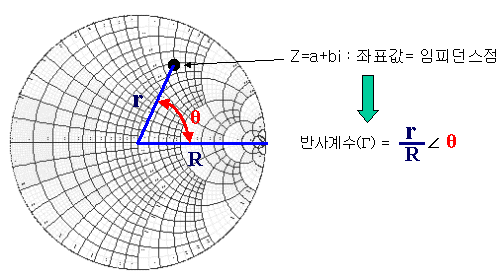
- 반지름 R, 중심에서 임의점까지의 거리 r은 반사계수를 의미
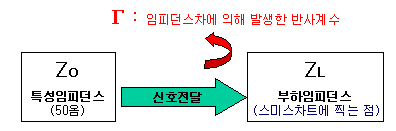
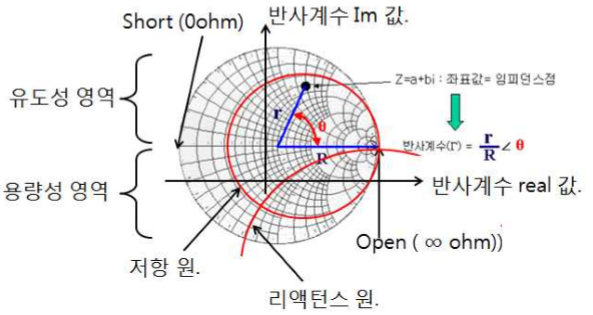
스미스 챠트 용도
- 주파수에 따른 임피던스 크기와 위상 측정
- 필터, 안테나, 소형 증폭기, 전송 선로 등의 특성 임피던스 파악
- 임피던스와 반사계수 관계
- 임피던스 매칭
https://ensxoddl.tistory.com/m/406
스미스차트 좌표상의 점이 의미하는 것은 임피던스
스미스차트의 중심점이 곧 특성임피던스를 의미하게 된다는 것
스미스 차트 중심점의 좌표는 1+j0 이기 때문
어떤 특성임피던스에서도 동일하게 적용하기 위해 1이라는 임피던스 점을 기준으로 함
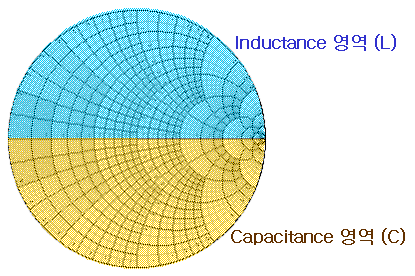
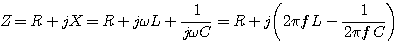
S11이 어느점에 존재하느냐=현재 부하임피던스가 인덕턴스 성분을 갖고 있는지, 캐패시턴스 성분을 갖고 있는지
주파수별로 나타날 때, S11 궤적이 위와 아래를 걸치게 된다는 것은, S파라미터 플롯상에서는 어떤 극점을 가진다는 의미
=올라가다가 내려가던지 내려가다가 올라가던지 하는 위치가 된다는 것
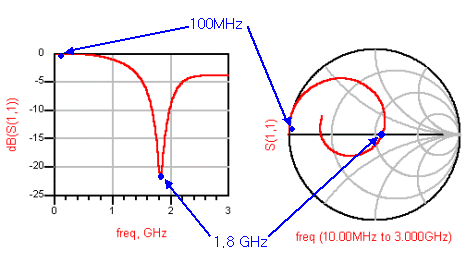
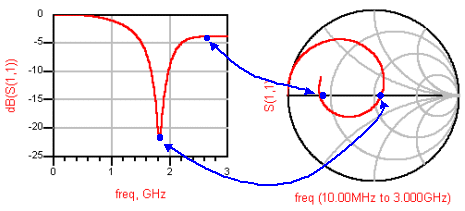
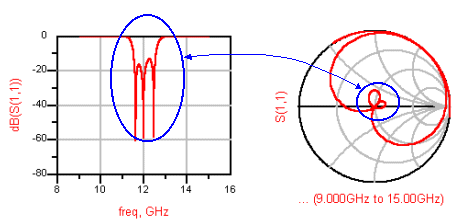
임피던스점=반사계수의 원리에 의해 S11이 낮을수록 (즉 반사가 적을수록) 스미스차트상의 점들은 중앙부에 모이고, S11이 높을수록(반사가 많이 될수록) 중앙에서 멀어지고 흩어집니다.
Filter의 S파라미터를 plot한 것으로서, S11이 떨어지는 통과대역 주파수의 임피던스점들은 스미스차트에서 중앙부에 위치하고 있음을 알 수 있습니다. 임피던스 점의 반사계수 읽는 법에서 알 수 있듯이, 중앙부에 가까울수록 반사계수가 작다는 의미이므로 당연한 것이지요.
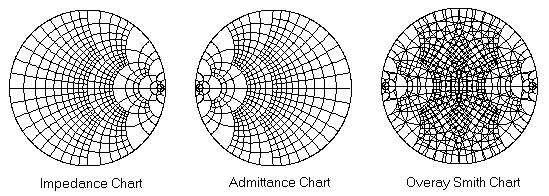
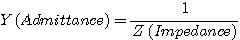
어드미턴스(Admittance)는 아시다시피 임피던스의 역수를 의미
임피던스는 얼마나 신호의 흐름을 방해하느냐의 기준이 되는 것에 반해 어드미턴스는 얼마나 신호를 더 잘 흘러줄 수 있느냐
결국 병렬 회로 구성을 위해 필요한 개념
직렬회로와 함께 병렬회로를 분석하고자 할 때는. 병렬단에서 어드미턴스라는 개념을 쓰는게 더하고 빼기가 훨씬 쉬워진다는 점이 중요합니다.
Short는 신호가 완전히 도통되게 단락되는 경우를 말하고, Open은 말그대로 회로가 끊어져서(열려서) 신호가 통과하지 못하는 상태를 말합니다.
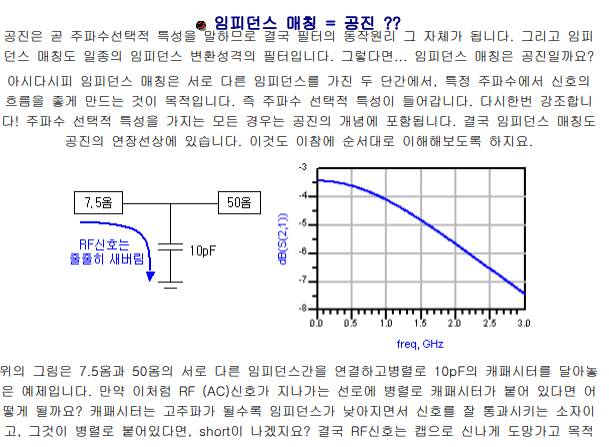
임피던스의 허수부가 아니라 실수부가 주로 결정하는 문제
임피던스가 0에 가까울수록 저항성분이 없다는 얘기이므로 신호가 자~알 흐르게되어 short가 됩니다. 반면 임피던스가 수백수천을 넘어 무한 대에 가까워지면 loss가 너무 심해서 신호가 흐르지 못하는 Open 상태가 되어버립니다. 이것은 스미스차트에서 아래처럼 보여집니다.
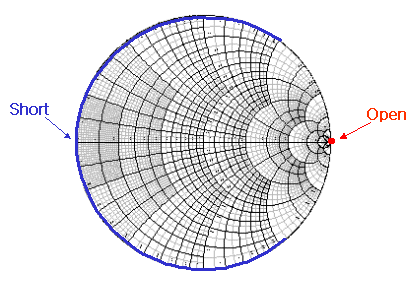
임피던스 점이 왼쪽에 있으면 낮은 임피던스, 오른쪽으로 가면 높은 임피던스점을 의미하게 됩니다. 이러한 점들은 좌표만 읽을 줄 알아도 바로 알 수 있는 것이므로 외우지 말고 이해하도록 하세요. 처음에 배울 때는 뭐가 뭔지 몰라서 마냥 외우기만하는 경우가 많은데, 임피던스가 0 인 원은 short가 되고, ∞ 인 원은 open이 된다는 것을 잘 음미해보시기 바랍니다.
http://www.rfdh.com/bas_rf/begin/smith2.htm
※ 복소수 `반사계수` 및 그에 해당하는 `임피던스`를 중첩시킨 극좌표계 표현 형식
- 복소 반사계수 평면(Γ 평면) 위에,
- 그에 상응하는 정규화된 저항(0 ≤ r ≤ ∞) 및 리액턴스(-∞ ≤ x ≤ ∞)를,
- 극좌표 형식으로 나타낸 챠트
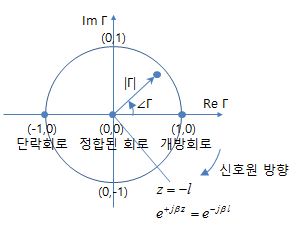
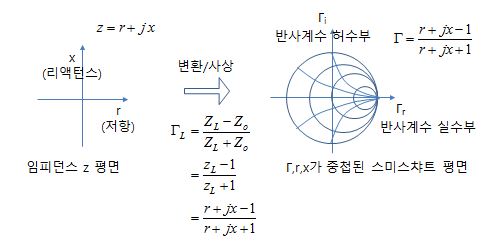
ㅇ 반사계수를 복소수 극 좌표계(Polar Coordinates)에 표시
- 반사계수 크기 |Γ| < 1 : 도표 중심점으로부터 원형으로 그려짐
- 반사계수 위상 -180˚< θ< 180˚ : 수평방향 우측선으로부터 측정되는 각도
http://www.ktword.co.kr/test/view/view.php?m_temp1=5476
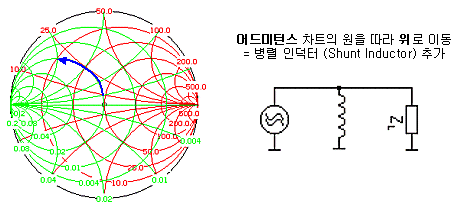
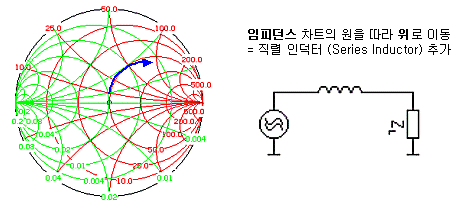
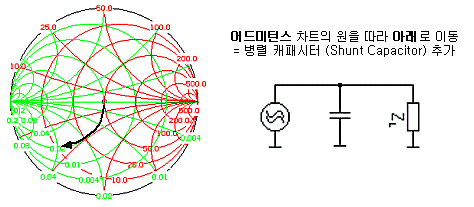
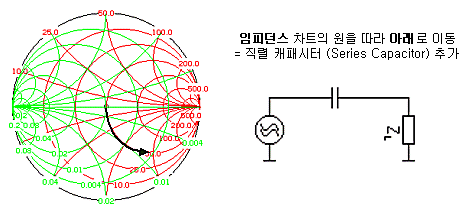
이 말을 간단히 정리하면
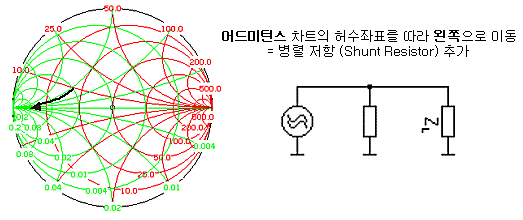
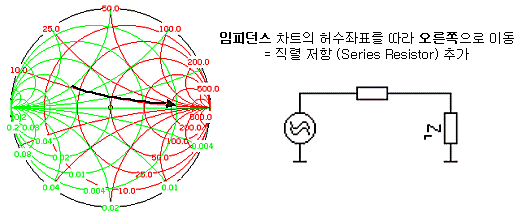
https://enjoyaudio.kr/zbxe/index.php?mid=questions&document_srl=7060567 http://www.rfdh.com/bas_rf/begin/smith4.htm
산란계수(S-parameter)
- 특정주파수에서 입력전압대 출력전압의 비를 의미한다.(주파수 영역에서 바라보는 파라미터)
- 2 port 네트워크에서 S-parameter는 S11, S12, S21, S22로 표현함
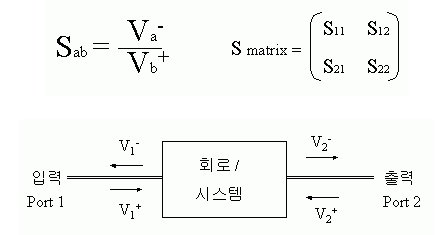
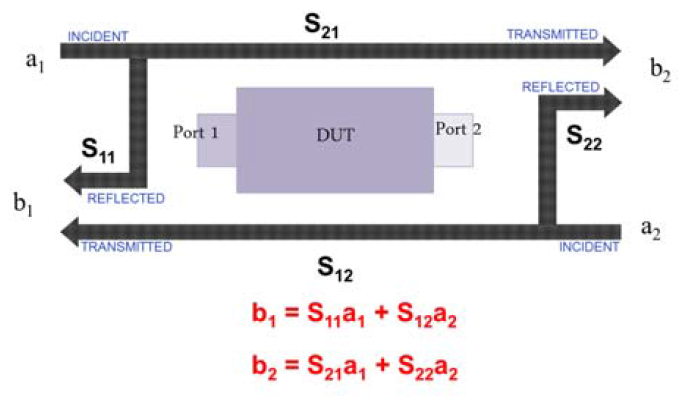
- 고주파(높은주파수)에서는 신호의 변화가 너무 빨라, 전압과 전류를 측정하기 어려움 이를 극복하기 위해 입력전압 대 출력전압 의 비로 측정합
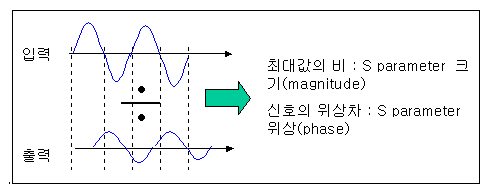
2. 고주파에서 S-Parameter를 사용하는 이유
- 주파수영역에서 신호에너지분포 확인이 용이함
- 고주파신호에 대한 측정/평가 하기가 용이함
<참조>
- 주파수가 올라갈수록 파형변화가 너무 빨라서 어떤 시점의 절대적인 전압, 전류값을 잡아내기 어려움, 즉 전압 전류를 측정하기가 곤란함
- 해결법은 바로 상대적인 값을 잡아 버리는 것입니다! 입력 전압파형이 들어갔을 때 출력 전압파형을 잡고, 그것을 실시간으로 측정하고 그 신호값을 서로 나누게 만드는 것, 그럼 최대값의 비와 두 신호의 위상차를 구할 수 있음]
- 이러한 계산을 해주는 것이 네트워크 아날라이져(Network Analyser)
- 내부에 Freq. synthesizer가 있어서 원하는 주파수대역에 설정한 만큼의 number of point수만큼의 주파수를 생성해서 일일이 각 주파수마다 그 S파라미터 값의 크기와 위상을 체크하고, 그것들을 연결해서 도표로 보여주는 것
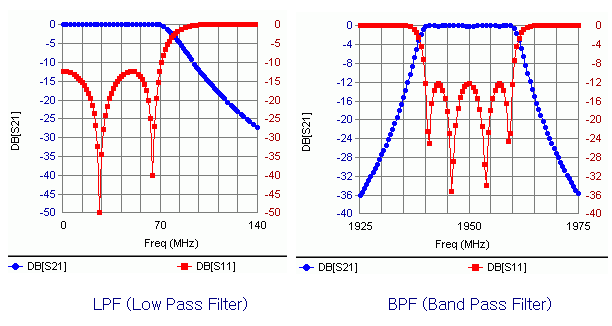
3. S-parameter 응용 및 예
- 필터해석에 응용
- 증폭기해석에 응용
- 임피던스매칭에 응용
https://ensxoddl.tistory.com/20
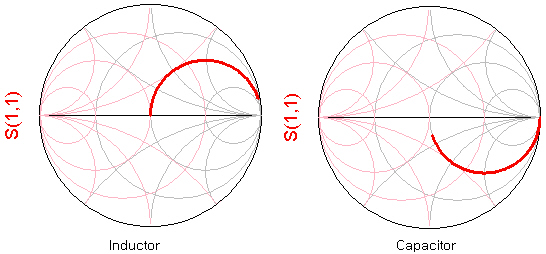
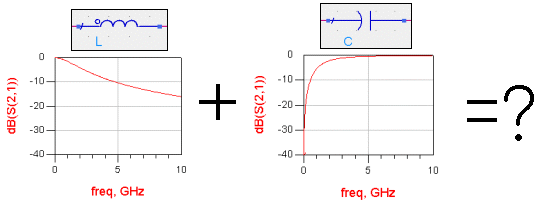
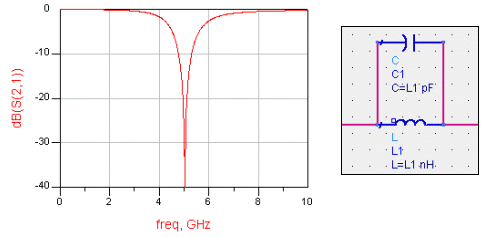
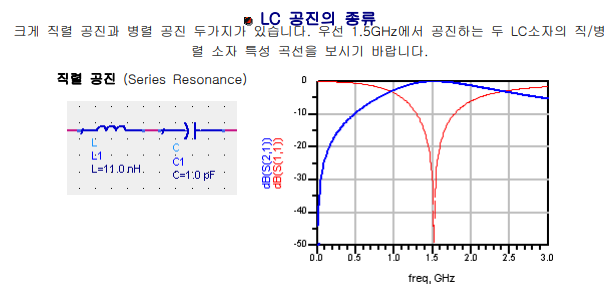
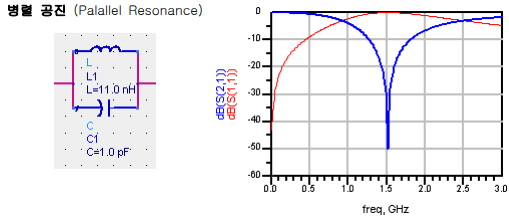
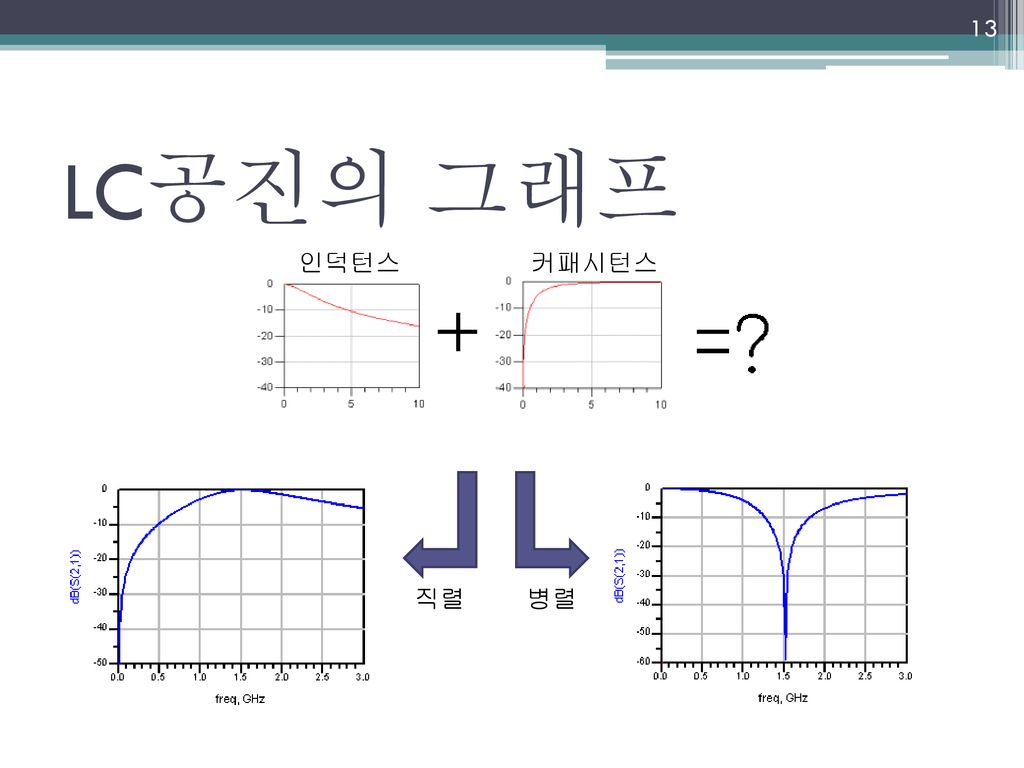
같은 LC값의 경우에는 공진주파수는 동일합니다. 그런데 S파라미터는 정 반대 로 동작하고 있는 것을 볼 수 있습니다. LC 직렬공진은 Bandpass (대역통과) 형태의 공진이 발생하고, LC 병렬공진은 Bandstop (대역저지) 형태의 공진이 발생합니다. 이렇듯 LC공진은 어떻게 연결하느냐에 따라 정반대의 특성이 나타날 수 있습니다.
그리고 L과 C가 평형을 이루면서 특정 주파수에 대한 선택적 특성을 갖게되는 바로 그 지점.. 그것을 우리는 공진(resonance) = LC 공진= 주파수가 선택적 특성을 가지는 현상
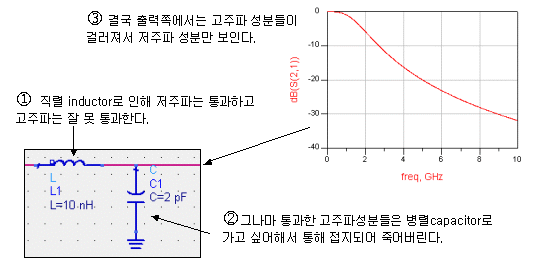
L과 C 자체를 잘 생각해보면 각각 Lowpass 특성과 Highpass 특성을 갖고 있다는 것을 눈치챌 수 있지요. 그걸 좀더 다듬고 조합해서 원하는 주파수, 원하는 감쇄 특성을 가지는 어떤 구조를 만든 것, 그것이 바로 ' Filter ' 입니다.
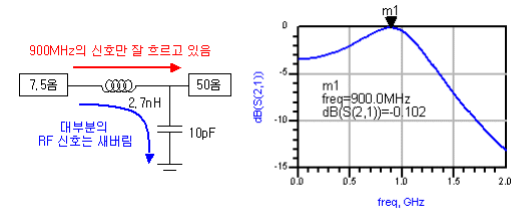
HPF의 경우는 L과 C의 소자 위치를 정반대로 바꾼 것
SRF (Self Resonating Frequency)
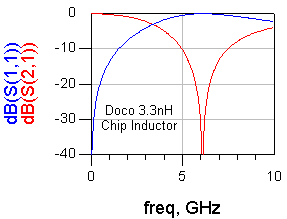
사실 지금까지 위에 언급한 L과 C에 대한 내용은 모두 ideal한 경우였습니다. 실제로 inductor와 capacitor를 사용할 때 꼭 알아두어야 할 것이, 바로 SRF(자기공진주파수)입니다. 아래는 실제 Inductor의 S21을 나타낸 그림
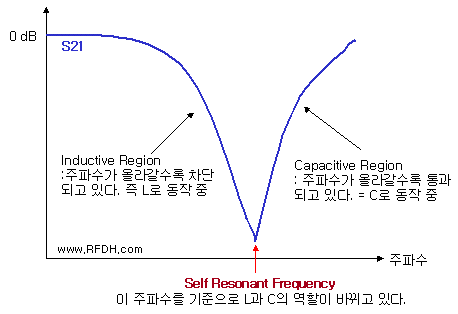
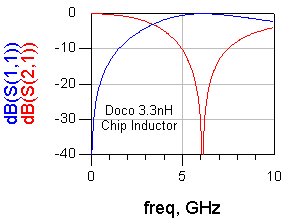
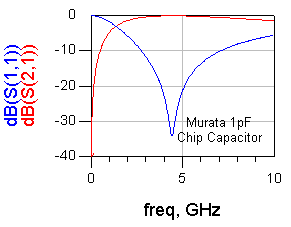
Inductor건 Capacitor건 특정 주파수를 넘어 버리면 자신의 역할이 반대로 뒤집어진다는 것입니다. Inductor가 Capacitor로 동작해 버리고, Capacitor가 Inductor로 동작해 버리는 황당한 상황이 발생한다는 것이지요. 그래서 이렇게 역할이 깨져버리는 주파수점이 마치 공진점과 같기 때문에 Self Resonating Frequency라 불리우는 것입니다
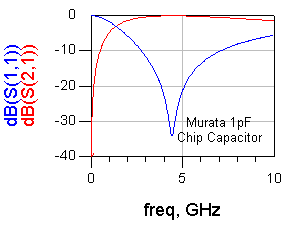
그래서 모든 Inductior, Capacitor를 사용할 때는 반드시 SRF보다 어느정도 낮은 주파수에서 사용해야 하며, 특히 Inductor 쪽에서 더 주의를 요합니다. 아래는 실제 소자의 Inductor와 Capacitor의 S 파라미터그래프를 보여준 것입니다. 둘다 특정 주파수 이후로 본연의 기능을 잃고 반대의 소자로 동작하고 있습니다.
Inductor와 Capacitor에서의 Q값이란 아래와 같은 의미입니다.
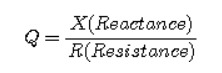
즉, 임피던스의 허수부/실수부를 말합니다. 임피던스의 허수부는 L, C 값을 의미하며 실수부는 저항값을 의미하지요. 결국 이게 무엇을 의미하느냐? 소자의 loss가 얼마이냐 입니다. 리액턴스 X는 L과 C 같은 무손실성 저장성분을 말합니다. 그냥 전기장 혹은 자기장의 형태로 주파수별로 에너지를 축적하는 기능이죠. 반면 분모에 있는 R값은 저항값, 즉 저항에 의한 손실을 의미합니다.
Q(Quality Factor)
결국 Q값이 클수록 loss가 적다는 의미
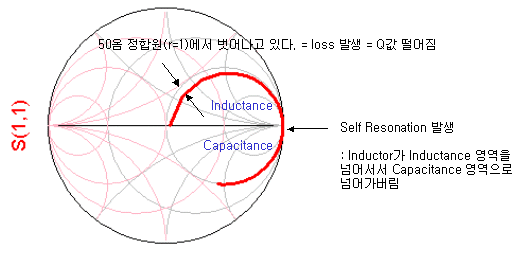
그림에 나와있듯이 Q값이 떨어져서, 즉 R값이 증가하면 손실이 늘고 결국 R=1 로 normalize된 실수 임피던스 원과 거리가 멀어지게 됩니다. 또한 Inductor로 동작해야할 이놈이 어느 주파수를 넘어서면서는 임피던스가 아래쪽 capacitance 영역으로 내려가 버렸습니다. 이렇게 L영역과 C영역을 넘어가는 그 포인트의 주파수가 바로 저 위에 설명한 SRF가 되는 것이지요.
SRF가 Inductor와 Capacitor의 이용범위를 알 수 있는 성능지표라면, Q값은 그 소자의 품질을 평가하는 아주 중요한 지표입니다
https://m.cafe.daum.net/kis0901/JrNO/2724
s파라미터에서는 왜 dB단위를 쓸까
상대적인 결과값이기 때문이다
https://m.blog.naver.com/wisdom0719/221261894963
스미스차트: 임피던스 매칭을 도와주는 하나의 도구
신호를 보내주는 부분과 신호를 출력해 주는 안테나의 부분을 연결시 정재파 발생
정재파: 진행파와 반사파가 동시에 존재하는 신호파
반사하는 신호가 많아지면 신호 약해짐
임피던스매칭 = 최대 출력 신호를 보내고자 함
특성임피던스 Z0=부하임피던스 ZL
Z=R+jX
Y=G+jB
Resistance 저항
G conductance 저항의 역수(전류를 잘 흐르게 하는 성분)
저항+임피던스
어드미턴스+서셉턴스
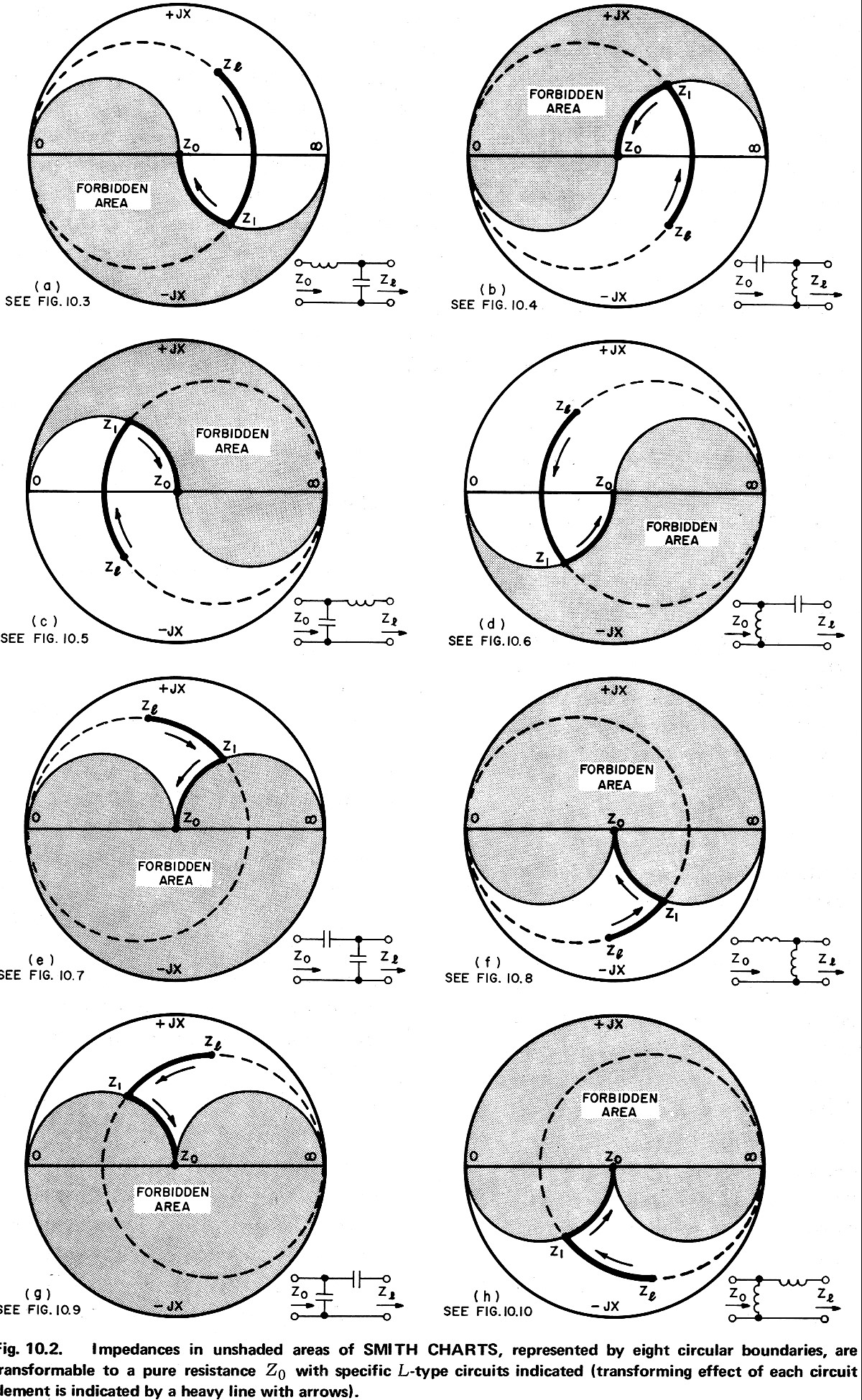
Z0>ZL의 경우
특성 임피던스가 크다
특성 임피던스 줄이고, 부하 임피던스 증가
특 병, 부 직
그림1
그림2
병렬 부분을 직렬로 표현하기 위해 어드미턴스화 한다
그림3
반대 상황
부하/특 = 1이 정합된 상태
부/특 = 알파를 1로 만드는 것이 임피던스 매칭
정규화 과정 필요
어떠한 값을 미리 정해진 기준의 값 안에 들도록 그 값의 범위를 조절
스미스차트의 단위 안에 표현할 수 있도록 단위 조절해 주는 과정
매칭 후 실제물리적인 값을 알기 위해서는 초기 특성 임피던스를 다시 곱해 줘야 함
임피던스 매칭 후 부하 임피던스는
특성 임피던스로 나누었을 때의 값이 1이기 때문에 부하임피던스=특성임피던스가 된다
이 말은 즉
50 = 50 + j50이고
허수부가 사라짐
차트 정 중앙
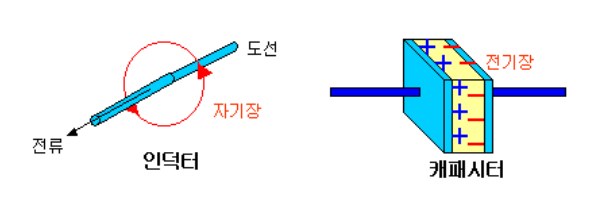
인덕터
직류 흘리고 교류 차단
전압의 위상이 전류의 위상보다 뒤처지게 하는 소자
커패시터
직류 차단 교류 ㅇ
전압의 위상이 전류의 위상보다 앞서게 하는 소자
스미스차트 = 임피던스 + 어드미턴스 차트
리액턴스 감소= 커패시터 직렬=회로가 용량성
리액턴스 증가=인덕터 직렬=회로가 유도성
서셉 증가=커패시터 직렬=회로 용량
서셉턴스 감소=인덕터 직렬=회로가 유도
반사계수 0
신호의 반사를 0퍼센트로 줄임
정합
전력의 효율을 최대화
https://m.blog.naver.com/daum4066546/220438516413
https://realordinarylife.tistory.com/4
산란계수(S-Parameter)에 대하여 설명하고 반사손실과 삽입손실을 설명
1. 산란계수(S-parameter) 2. 고주파에서 S-Parameter를 사용하는 이유 3. S-parameter 응용 및 예 4. 삽입 손실(Insertion loss) 5. 반사 손실(Return loss) 6. 맺음말 1. 산란계수(S-parameter) - 특정주파수에서 입력전압
ensxoddl.tistory.com
http://contents2.kocw.or.kr/KOCW/document/2016/honam/yuntaesoon/3.pdf
http://ael.chungbuk.ac.kr/lectures/undergraduate/%EC%A0%84%ED%8C%8C%EA%B4%91%ED%8C%8C%EC%86%8C%EC%9E%90/lecture-notes/%EC%A0%9C2%EC%9E%A5-%EC%A0%84%EC%86%A1%EC%84%A0.pdf
http://contents2.kocw.or.kr/KOCW/document/2016/honam/yuntaesoon/3.pdf
https://k6jca.blogspot.com/2015/03/notes-on-antenna-tuners-l-network-and.html
https://slidesplayer.org/slide/15544435/
전송선 https://slidesplayer.org/amp/14701568/

'성장캐 > 제어공학' 카테고리의 다른 글
| [질문] 시정수를 음수일 때 역수로 두는 이유 (0) | 2022.07.06 |
|---|---|
| 주파수 영역 해석 Frequency-domain Analysis (1) | 2022.07.05 |
| 시스템의 극점과 영점이 시간 응답에 미치는 영향 (0) | 2022.07.05 |
| 시간 영역 해석 Time-Domain Analysis (0) | 2022.07.05 |
| 회로를 시간 영역이 아닌 주파수 영역에서 해석하는 이유가 뭘까 (0) | 2022.06.21 |






