Divide and Conquer
반복법(Jacobi 방법, Gauss-Seidel 방법) 본문
728x90
- 반복법
- 선형 연립방정식의 해를 찾을 때 초기값을 가정하여 반복되는 과정을 수행하여 해를 구하는 방법
- 한 번에 해를 찾을 가능성은 거의 없음
- 원하는 정확도의 해를 구하기까지 같은 과정을 반복
- 반복법의 종류
- Jacobi 방법
- Gauss-Seidel 방법

| Jacobi | Gauss-Seidel |
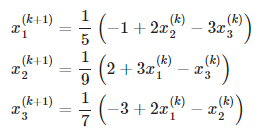 |
 |
 |
 |
| 새로운 값을 단계의 마지막에 한꺼번에 갱신 | 새로 계산한 값을 반복 계산 단계가 끝날 때까지 기다리지 않고 곧바로 갱신 |
| 근사값의 수렴속도가 보다 빠른 것을 기대할 수 있음 반드시 최적의 결과를 보장하는 것은 아님 |
# Jacobi
import numpy as np
import matplotlib.pyplot as plt
m = 10 # 반복횟수
x1j = np.zeros(m) # 초기값이 전부 0이야
x2j = np.zeros(m)
x3j = np.zeros(m)
print('%7s %9s %9s %9s'%('k', 'x1', 'x2', 'x3'))
print('%7d %9.5f %9.5f %9.5f'%(0, x1j[0], x2j[0], x3j[0]))
for k in range(m-1):
x1j[k+1] = (-1.0 + 2.0 * x2j[k] - 3.0*x3j[k]) / 5.0
x2j[k+1] = ( 2.0 + 3.0*x1j[k] - x3j[k]) / 9.0
x3j[k+1] = (-3.0 + 2.0*x1j[k] - x2j[k] ) / 7.0
print('%7d %9.5f %9.5f %9.5f'%(k+1, x1j[k+1], x2j[k+1], x3j[k+1]))
# 반복횟수를 눌리면 안 보이는 곳에서도 수렴k = np.arange(1, m+1)
plt.plot(k, x1j, 'b-o', label = '$x_1$')
plt.plot(k, x2j, 'r--v', label = '$x_2$')
plt.plot(k, x3j, 'g-.*', label = '$x_3$')
plt.legend()
plt.show()
eps1 = np.zeros(m-1)
eps2 = np.zeros(m-1)
eps3 = np.zeros(m-1)
for i in range(m-2):
eps1[i] = np.abs((x1j[i+1] - x1j[i])/x1j[i+1]) * 100.0
eps2[i] = np.abs((x2j[i+1] - x2j[i])/x2j[i+1]) * 100.0
eps3[i] = np.abs((x3j[i+1] - x3j[i])/x3j[i+1]) * 100.0
print(eps1)
plt.plot(k[:-1], eps1, 'b-o', label = '$\epsilon_1$')
plt.plot(k[:-1], eps2, 'r--v', label = '$\epsilon_2$')
plt.plot(k[:-1], eps3, 'g-.*', label = '$\epsilon_3$')
plt.legend()
plt.show()
# 6번 정도 반복했을 때 근삿값 얻어냄.
- 해가 존재해도 발산할 수 있음. 초기값을 바꿔볼 것.
- 대각선 우세 조건을 만족시키면 오차를 더욱 줄일 수 있음.
#Gauss-Seidel
import numpy as np
import matplotlib.pyplot as plt
m = 10
x1 = np.zeros(m)
x2 = np.zeros(m)
x3 = np.zeros(m)
print('%7s %9s %9s %9s'%('k', 'x1', 'x2', 'x3'))
print('%7d %9.5f %9.5f %9.5f'%(0, x1[0], x2[0], x3[0]))
for k in range(m-1):
x1[k+1] = (-1.0 + 2.0*x2[k] - 3.0*x3[k]) / 5.0
x2[k+1] = ( 2.0 + 3.0*x1[k+1] - x3[k]) / 9.0
x3[k+1] = (-3.0 + 2.0*x1[k+1] - x2[k+1] ) / 7.0
# x1[k+1], x2[k+1]처럼 바로 갱신된 것 확인 가능eps1 = np.zeros(m-1)
eps2 = np.zeros(m-1)
eps3 = np.zeros(m-1)
print('%7s %9s %9s %9s %9s %9s %9s'%('k', 'x1', 'x2', 'x3', 'eps1', 'eps2', 'eps3'))
print('%7d %9.5f %9.5f %9.5f %9s %9s %9s'%(0, x1[0], x2[0], x3[0], '', '', ''))
for k in range(m-1):
eps1[k] = np.abs((x1[k+1] - x1[k])/x1[k+1]) * 100.0
eps2[k] = np.abs((x2[k+1] - x2[k])/x2[k+1]) * 100.0
eps3[k] = np.abs((x3[k+1] - x3[k])/x3[k+1]) * 100.0
print('%7d %9.5f %9.5f %9.5f %9.2f %9.2f %9.2f'%(k+1, x1[k+1], x2[k+1], x3[k+1], eps1[k],eps2[k], eps3[k]))itr = np.arange(1, m+1)
plt.plot(itr, x1, 'b-o', label = '$x_1$')
plt.plot(itr, x2, 'r--v', label = '$x_2$')
plt.plot(itr, x3, 'g-.*', label = '$x_3$')
plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Approximate solutions')
plt.title('Gauss-Seidel method')
plt.show()
plt.plot(itr[:-1], eps1, 'b-o', label = '$\epsilon_1$')
plt.plot(itr[:-1], eps2, 'r--v', label = '$\epsilon_2$')
plt.plot(itr[:-1], eps3, 'g-.*', label = '$\epsilon_3$')
plt.legend()
plt.xlabel('Iterations')
plt.ylabel('Relative errors')
plt.show()
반응형
'성장캐 > 수치해석' 카테고리의 다른 글
| LU 분해 LU decomposition (0) | 2022.06.21 |
|---|---|
| 수치미분 numerical differentiation (0) | 2022.06.20 |
| Gauss 소거법 Gauss Elimination (0) | 2022.04.25 |
| 선형 연립방정식의 해법 (0) | 2022.04.25 |
| 할선법 Secant Method (0) | 2022.04.25 |
Comments



