Divide and Conquer
할선법 Secant Method 본문
728x90
미분을 안 해도 됨구간 안에 근이 존재하지 않아도 된다(초기값 2개)
할선과 𝑥 축과의 교점을 새로운 점으로 하여 근에 접근
할선(secant): 두 점을 이은 직선
접선, tangent, 법선 normal
Newton-Raphson 방법보다 수렴이 더 빠른 경우도 있다.
but 문제 동일(기울기를 쓰기 때문에 수렴 안 할 수도 있다)
오차를 구하기 위해 앱실론을 사용(상대오차)
eps, error
$$x^{(k+1)} =x^{(k)} - f(x^{(k)}){{x^{(k)} - x^{(k-1)}}\over{f(x^{(k)})-f(x^{(k-1)})}} $$
import numpy as np
def f(x):
return 3*x-np.cos(x)-1
n = 7
xs = np.zeros(n) # 근사값
eps = np.zeros(n)
trueValue = 1.0 #해석적 방법으로 구한 참값
x0 = -3.0
x1 = 4
for k in range(n):
x2 = x1 - f(x1) * ((x1-x0)/(f(x1) - f(x0)))
x0 = x1
x1 = x2
xs[k] = x2
if k >= trueValue:
eps[k] = (xs[k]-xs[k-1])/xs[k] # *100.0
# 실제 근은 5.0과 1.0
print("%5s %8s %8s"%('k', 'x', 'eps'))
for k in range(n):
print("%5d %9.4f %12.9f"%(k+1, xs[k], eps[k]))import matplotlib.pyplot as plt
#%matplotlib inline
x = np.linspace(-3.0, 4.0, 50) # np.linspace(2.0, 4.0, 50)
fx = f(x)
#fig, ax = plt.subplots()
for i in range(1, n):
plt.plot(x, fx) #기본그래프
plt.plot(xs, f(xs), 'xr')
plt.plot(xs[i-1:i+1], f(xs[i-1:i+1]), 'g')
plt.grid()
plt.pause(0.5)
plt.show()
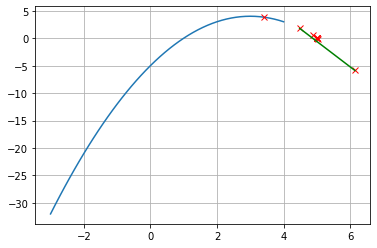




f(xs)
array([ 3.84000000e+00, -5.87755102e+00, 1.79812695e+00, 4.93706449e-01,
-7.88037095e-02, 2.56829070e-03, 1.25303412e-05, -2.01200123e-09,
0.00000000e+00, 0.00000000e+00])
반응형
'성장캐 > 수치해석' 카테고리의 다른 글
| Gauss 소거법 Gauss Elimination (0) | 2022.04.25 |
|---|---|
| 선형 연립방정식의 해법 (0) | 2022.04.25 |
| 뉴튼랩슨 Newton-Raphson (0) | 2022.04.25 |
| 고정점 방법 Fixed point Method (0) | 2022.04.25 |
| 이분법 Bisection method (0) | 2022.04.25 |
Comments



